Generating Biquad IIR Filter Coefficients¶
This example demonstrates creating a biquad coefficient set filtering the input to the derivative component (Kd) of the PID.
import numpy as np
def ConvertShiftedBinToDouble (num, shift=32):
"""
Take a fixed point and convert to a double
"""
ShiftBy = long(0x1L) << shift
return (num / float(ShiftBy))
def ConvertDoubleToShiftedBin (val, shift=32):
"""
Take a double and convert to a fixed point
"""
ShiftBy = long(0x1L) << shift
ShiftedVal_d = (val * ShiftBy)
ShiftedVal = (round(ShiftedVal_d))
return long(ShiftedVal)
def compute_biquad_coeff(filter_type, freq_cutoff, freq_samplerate, Q=0.7071):
"""
Returns coefficients a0,a1,a2,b1,b2
*filter_type* - the string name of the filter type (lowpass, highpass, bandpass, notch)
See constant BIQUAD_FILTER_TYPE_NAMES
*freq_cutoff* - the filter cutoff frequency of filter in Hz.
*freq_samplerate* - the sampling rate of the biquad filter.
see also: http://www.earlevel.com/main/2012/11/26/biquad-c-source-code/
http://www.earlevel.com/main/2003/02/28/biquads/
http://www.earlevel.com/main/2011/01/02/biquad-formulas/
"""
k = np.tan(np.pi * freq_cutoff / freq_samplerate)
if filter_type == "lowpass":
norm = 1 / (1 + k / Q + k * k);
a0 = k * k * norm;
a1 = 2 * a0;
a2 = a0;
b1 = 2 * (k * k - 1) * norm;
b2 = (1 - k / Q + k * k) * norm;
elif filter_type == "highpass":
norm = 1 / (1 + k / Q + k * k);
a0 = 1 * norm;
a1 = -2 * a0;
a2 = a0;
b1 = 2 * (k * k - 1) * norm;
b2 = (1 - k / Q + k * k) * norm;
elif filter_type == "bandpass":
norm = 1 / (1 + k / Q + k * k);
a0 = k / Q * norm;
a1 = 0;
a2 = -a0;
b1 = 2 * (k * k - 1) * norm;
b2 = (1 - k / Q + k * k) * norm;
elif filter_type == "notch":
norm = 1 / (1 + k / Q + k * k);
a0 = (1 + k * k) * norm;
a1 = 2 * (k * k - 1) * norm;
a2 = a0;
b1 = a1;
b2 = (1 - k / Q + k * k) * norm;
return a0,a1,a2,b1,b2
def convert_biquad_coeff_fixedpoint(coef):
"""
Given a set of coeff convert to fixed point (integer) with
a shift amount (shiftby)
"""
bitwidth = 32
numcoef = 5
fixedcoef = []
localshiftby = 0
absmaxscaled = (1 << (bitwidth-1)) - 1
maxval = np.max(np.absolute(coef))
if maxval == 0.: # error
return coef
scalefactor = absmaxscaled / maxval
# find next lowest power of two
for i in range(31,-1,-1):
print i
if (1 << i) & long(scalefactor):
scalefactor = 1 << i
localshiftby = i
break
for i in range(0,numcoef):
fixedcoef.append(ConvertDoubleToShiftedBin(coef[i],localshiftby))
return localshiftby, fixedcoef
def compute_biquad_freq_response(coef, freq_samplerate):
"""
Returns two 1-D ndarrays of x and y in a tuple. x is in terms of Hz and
y is in dB if *db* is True.
*coef* - the coefficients of the filter
*freq_samplerate* - the sampling rate of the filter.
"""
a0,a1,a2,b1,b2 = coef
n = 100
w = np.linspace(0,np.pi,n)
np.power(np.sin(w/2.), 2)
y = np.log(np.power(a0+a1+a2, 2) - 4.*(a0*a1 + 4.*a0*a2 + a1*a2)*np.power(np.sin(w/2.), 2) + 16.*a0*a2*np.power(np.sin(w/2.), 4)) - np.log(np.power(1.+b1+b2, 2) - 4.*(b1 + 4.*b2 + b1*b2)*np.power(np.sin(w/2.), 2) + 16.*b2*np.power(np.sin(w/2.), 4))
y = y * 10. / np.log(10)
#x = np.linspace(0,freq_samplerate/2.,n)
return ((freq_samplerate*0.5/np.pi)*w, y)
def compute_and_write_biquad_coeff(pd, filter_type, freq_cutoff, freq_samplerate, Q=0.7071):
"""
Compute a set of coefficients and write them to the PiMotion.
*pd* - Connection to a PiMotion device (ex: pd = pilib.PiDev('ip_address'))
*filter_type* - the string name of the filter type (lowpass, highpass, bandpass, notch)
See constant BIQUAD_FILTER_TYPE_NAMES
*freq_cutoff* - the filter cutoff frequency of filter in Hz.
*freq_samplerate* - the sampling rate of the biquad filter.
Calculated as:
freq_samplerate = int(pilib.DEFAULT_CLK_PIMOTION / elec_cycle_div)
"""
# generate a biquad filter coef set
coef = compute_biquad_coeff(filter_type, freq_cutoff, freq_samplerate)
# get fixed point coef (integer)
shiftby,fixedcoef = convert_biquad_coeff_fixedpoint(coef)
pd.mtr_set_biquad_enable(0) # disable the active biquad filter
pd.mtr_set_biquad_a0(fixedcoef[0]) # write the coefficients
pd.mtr_set_biquad_a1(fixedcoef[1])
pd.mtr_set_biquad_a2(fixedcoef[2])
pd.mtr_set_biquad_b1(fixedcoef[3])
pd.mtr_set_biquad_b2(fixedcoef[4])
pd.mtr_set_biquad_shiftby(shiftby) # write the shift amount
pd.mtr_set_biquad_enable(1) # enable the biquad filter
class biquad_filter():
"""
Implement a biquad filter in software
"""
def __init__(self):
self.z1 = 0.
self.z2 = 0.
self.z1_f = 0
self.z2_f = 0
def process(self,x,coef):
"""
Process a single point and return the filtered result
"""
a0,a1,a2,b1,b2 = coef
result = (x * a0) + self.z1
self.z1 = (x * a1) + self.z2 - (b1 * result)
self.z2 = (x * a2) - (b2 * result)
return result
def processfixed(self,x,coef,sb):
"""
Process a single data point given fixed point coeff and return the
filtered result
"""
a0,a1,a2,b1,b2 = coef
result = ((x * a0)>>sb) + self.z1_f
self.z1_f = ((x * a1)>>sb) + self.z2_f - ((b1 * result)>>sb)
self.z2_f = ((x * a2)>>sb) - ((b2 * result)>>sb)
return result
if __name__ == '__main__':
"""
Test the biquad filter coef
"""
import pylab
import matplotlib.pyplot as plt
filter_type = "lowpass"
freq_samplerate = 1000. # Sampling rate of the signal in Hz (update rate of the servo)
freq_cutoff = 50. # Hz
# generate a biquad filter coef set
coef = compute_biquad_coeff(filter_type, freq_cutoff, freq_samplerate, Q=0.7071)
# create a biquad filter frequency response plot
x_freq_resp,y_freq_resp = compute_biquad_freq_response(coef,freq_samplerate)
pylab.figure(1,facecolor="white")
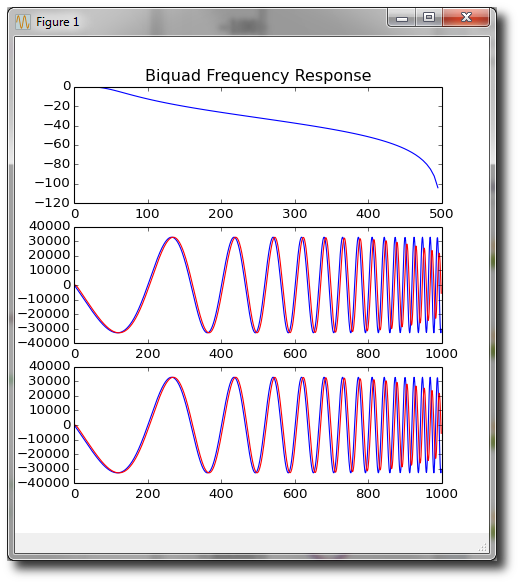
plt.subplot(311)
plt.title("Biquad Frequency Response")
pylab.plot(x_freq_resp,y_freq_resp)
# create a sweep waveform
t = np.linspace(0, 1, freq_samplerate, endpoint=False)
sw = np.sin(np.pi*np.logspace(0,1.5,freq_samplerate))
# convert to 16bit integer
sw = sw*32768
sw = sw.astype(int)
# get fixed point coef (integer)
shiftby,fixedcoef = convert_biquad_coeff_fixedpoint(coef)
print 'shiftby =',shiftby, 'coef = ', fixedcoef
# conpare fixedpoint coef to original
for (fc,c) in zip(fixedcoef,coef):
print fc,ConvertShiftedBinToDouble(fc,shiftby),c
# run the simulated waveforms through the biquad filter with fixed
# point and floating point coef
bq = biquad_filter()
x = []
for s in sw:
# filter with floating point coef
x.append(bq.process(s,coef))
x_f = []
for s in sw:
# filter with fixed point coef
x_f.append(bq.processfixed(s,fixedcoef,shiftby))
# plot the sweep with filtered data using floating point coef
plt.subplot(312)
pylab.plot(sw,'b')
pylab.plot(x,'r')
# plot the sweep with filtered data using fixed point coef
plt.subplot(313)
pylab.plot(sw)
pylab.plot(x_f,'r')
pylab.show()
An example using biquad.py in a PiMotion application:
import biquad.py
pd = pilib.Pidev('my_ip_address')
# compute the coeff and write them to the pimotion
compute_and_write_biquad_coeff(pd, 'lowpass', 100., 1000)
